시간 복잡도
- 시간 복잡도는 알고리즘이 입력 크기에 따라 소요되는 시간의 증가율을 나타내는 개념
- 입력 크기가 커질수록 알고리즘의 실행 시간이 어떻게 증가하는지를 나타낸다.
점근적 분석 (Asymptotic Analysis):
점근적 분석은 입력 크기가 충분히 클 때 알고리즘의 동작을 분석하는 것
알고리즘의 최악의 경우 시간 복잡도를 분석하여 입력 크기에 대한 함수로 표현한다.
- 주로 Big O 표기법을 사용하여 표현된다.
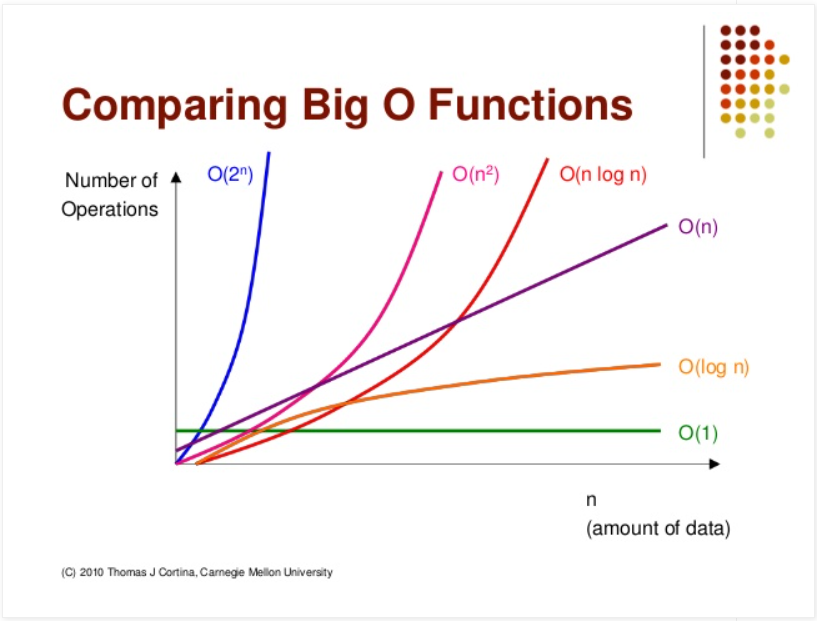
Big O 표기법 (Big O Notation):
Big O 표기법은 알고리즘의 시간 복잡도를 나타내는 표기법 중 하나
알고리즘의 시간 복잡도가 입력 크기에 대해 얼마나 빠르게 증가하는지를 상한으로 나타낸다.
예를 들어, O(n)은 입력 크기에 비례하여 선형적으로 증가한다는 것을 의미한다.
- 알고리즘의 최악의 경우 시간 복잡도를 분석하여 입력 크기에 대한 함수로 표현한다.
최선, 평균, 최악의 경우 (Best, Average, Worst Case):
알고리즘의 시간 복잡도는 주로 최선, 평균, 최악의 경우로 나뉜다.
최선의 경우는 알고리즘의 최적 동작 시나리오에서 소요되는 시간을 나타낸다.
최악의 경우는 알고리즘의 최악 동작 시나리오에서 소요되는 시간을 나타낸다.
시간복잡도 종류
1. 선형 탐색 (Linear Search)
- 선형 탐색은 주어진 리스트에서 찾고자 하는 값을 처음부터 끝까지 순차적으로 비교하여 찾는다.
- 요소를 하나씩 확인하면서 일치하는 값을 찾으면 해당 요소의 인덱스를 반환한다.
- 최악의 경우 모든 요소를 확인해야 하므로 O(n)
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i # 찾고자 하는 값의 인덱스 반환
return -1 # 찾고자 하는 값이 없는 경우 -1 반환
arr = [3, 6, 2, 8, 1, 7, 5]
target = 7
result = linear_search(arr, target)
print("찾고자 하는 값의 인덱스:", result)- 함수 linear_search는 입력으로 리스트 arr와 찾고자 하는 값 target을 받는다.
- 리스트의 각 요소를 순차적으로 확인하면서 찾고자 하는 값과 일치하는 요소를 찾는다.
- 만약 찾고자 하는 값이 발견되면 해당 요소의 인덱스를 반환합니다. 발견되지 않으면 -1을 반환한다.
2. 이진 탐색 (Binary Search)
- 이진 탐색은 정렬된 리스트에서 중간 요소를 선택하고 찾고자 하는 값과 비교하여 검색 범위를 반으로 줄
- 찾고자 하는 값이 중간 값보다 작으면 왼쪽 부분을, 크면 오른쪽 부분을 대상으로 탐색을 반복한다.
- 최악의 경우 리스트를 반으로 쪼개며 탐색하므로 O(log n)
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid # 찾고자 하는 값의 인덱스 반환
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1 # 찾고자 하는 값이 없는 경우 -1 반환
arr = [1, 2, 3, 5, 6, 7, 8]
target = 7
result = binary_search(arr, target)
print("찾고자 하는 값의 인덱스:", result)- 함수 binary_search는 입력으로 정렬된 리스트 arr와 찾고자 하는 값 target을 받습니다.
- 변수 left와 right는 탐색 범위의 왼쪽과 오른쪽 끝 인덱스를 가리킵니다.
- 탐색 범위를 반으로 나누어서 중간 요소를 확인하고, 찾고자 하는 값과 비교하여 탐색 범위를 조절합니다.
- 만약 찾고자 하는 값이 발견되면 해당 요소의 인덱스를 반환합니다. 발견되지 않으면 -1을 반환합니다.
3. 버블 정렬 (Bubble Sort)
- 버블 정렬은 인접한 두 요소를 비교하고 필요에 따라 교환하여 가장 큰 요소를 배열의 끝으로 이동시킨다.
- 이러한 과정을 배열의 모든 요소에 대해 반복하면서 정렬을 완성한다.
- 최악의 경우 모든 요소를 비교하므로 O(n^2)
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [5, 3, 8, 4, 2]
bubble_sort(arr)
print("정렬된 배열:", arr)- 함수 bubble_sort는 입력으로 리스트 arr를 받는다.
- 이중 반복문을 사용하여 인접한 두 요소를 비교하고 필요에 따라 교환하여 가장 큰 요소를 배열의 끝으로 이동시킨다.
- 이러한 과정을 반복하여 배열을 정렬한다.
- 이 코드는 입력 리스트를 직접 수정하며, 정렬된 배열이 반환되지 않고 원래 리스트가 변경된다.
정리
- 시간 복잡도는 알고리즘의 효율성을 평가하는 중요한 지표이며, 입력 크기에 따라 알고리즘의 성능을 예측하는 데 사용된다.
- Big O 표기법을 통해 알고리즘의 시간 복잡도를 간단하고 명확하게 표현할 수 있다.
관련 용어
1. 상수 시간 (Constant Time)
- 입력 크기와 상관없이 일정한 시간만큼 소요되는 알고리즘의 경우를 말한다.
- 시간 복잡도 : O(1)
2. 선형 시간 (Linear Time)
- 입력 크기에 비례하여 시간이 선형적으로 증가하는 알고리즘의 경우를 말한다.
- 시간 복잡도 : O(n)
3. 로그 시간 (Logarithmic Time)
- 입력 크기의 로그에 비례하여 시간이 증가하는 알고리즘의 경우를 말한다.
- 시간 복잡도 : O(log n)
4. 지수 시간(Exponential Time)
- 알고리즘의 실행 시간이 입력 크기에 대해 지수적으로 증가하는 경우를 말한다.
- 시간 복잡도 : O(2^n) 또는 O(n^2)
'CS' 카테고리의 다른 글
| 소프트웨어 개발 방법론(Scrum, 차이점) (0) | 2024.04.17 |
|---|---|
| 소프트웨어 개발 방법론(폭포수 모델, Agile 방법론) (0) | 2024.04.16 |
| 캐시 메모리(Cache Memory) (0) | 2024.04.11 |
| OSI(Open Systems Interconnection) (0) | 2024.04.10 |
| 가비지 컬렉션(Garbage Collection) (0) | 2024.04.09 |

